[정수론] 소수판별

목차

---

[단일대상 소수판별]

1. 기본 소수판별법 -> O(N)

2. 개선된 소수판별법 -> O(N^1/2)

3. 더 개선된 소수판별법 -> O(N^1/2) * K (K<=0.5) 

4. 밀러-라빈 소수판별법 -> O(K(logN)^3) ~ O(K(logN)^2)

 

[구간대상 소수판별]

1. 개선된 소수판별법 + 브루트포스 -> O(N * N^1/2) 

2. 에라토스테네스의 체 -> O(Nlog(logN))

 

[소인수분해]

1. 개선된 소수판별법 + 브루트포스 -> O(N^1/2)

2. 브루트포스 + 전처리/예외처리 -> O(NlogN)

3. 폴라드로  -> O(N^1/4)

 

---

<단일대상 소수판별>

단일대상 소수판별법은, 대개 다음과 같은 상황에서 사용됩니다.

-> 입력은 한개의 정수가 들어오며, 이것이 소수인지 판별하는 경우

입력이 N개 들어온다면, <단일대상 소수판별법>의 시간복잡도에 N을 곱한 시간이 소요됩니다.

이는 뒤에 다룰 <구간대상 소수판별법>과의 시간복잡도를 비교할 필요가 있습니다.

 

1. 기본 소수판별법 (Trial division)

bool isPrime(int n) {
    if (n <= 1)return false;
    if (n == 2)return true;
    for (int i = 2; i <= n - 1; i++)
        if (n % i == 0)return false;
    return true;
}

 

소수의 정의를 활용하여, 소수를 판별할 수 있습니다.

1과 n만을 인수로 갖는다는것은, [2, n-1]에 인수가 존재하면 합성수로 판단할 수 있습니다.

시간복잡도는 O(N)입니다.

 

2. 개선된 소수판별법(Trial division)

bool isPrime(int n) {
    if (n <= 1)return false;
    if (n == 2)return true;
    for (int i = 2; i * i <= n; i++)
        if (n % i == 0)return false;
    return true;
}

 

아래의 명제가 참임을 이용해서 같은 로직이여도, 가지치기를 통해 시간복잡도를 개선할 수 있습니다.

-> 모든 합성수는 sqrt(N)이하의 인수를 갖는다

시간복잡도는 O(sqrt(N))입니다.

 

3. 더 개선된 소수판별법(Wheel factorization)

bool isPrime(int n) {
    if (n <= 1)return false;
    if (n == 2)return true;
    if (n % 2 == 0)return false;
    for (int i = 3; i * i <= n; i+=2)
        if (n % i == 0)return false;
    return true;
}

(1)과 (2)에서 사용된, 소수의 정의를 사용한 로직을 그대로 유지하며 더 개선해볼 수 있습니다.

 

위 코드는 2에 대해서만 Wheel factorization을 적용하였습니다. 모든 짝수를 건너뛰므로, 전체의 50%입니다.

만약 {2, 3}에 대해서 Wheel factorization을 적용하면 대상수는 1/3이 되어 전체의 33%를 탐색합니다.

같은 방식으로 {2, 3, 5}이면 27%, {2, 3, 5, 7}이면 23%정도의 수에대해서만 탐색을 진행하게 됩니다.

즉, 초반 몇개의 수에 대해서 미리 예외처리를 해두고,

이를 바탕으로 일부 숫자를 건너뛰는것이 Wheel factorization입니다.

※ Wheel factorization은 '에라토스테네스의 체'의 최적화에서도 요긴하게 사용됩니다.

 

---

지금까지 다룬 소수판별법을 '결정론적 소수판별법'이라 부릅니다.

한마디로 결정을 지어버린다는 것인데,

결정론적 소수판별법의 범주안에 들어가는 알고리즘에서 어떤 수가

소수로 판별되면 그 수는 무조건 소수이고, 합성수로 판별되면 그 수는 무조건 합성수란 뜻입니다.

 

반대로 결정론적 소수판별법이 아닌 소수판별법도 있습니다. 이를 '확률론적 소수판별법'이라 부릅니다.

※ 확률론적 알고리즘의 다른 이름으로는, '확률적 알고리즘' 혹은 '무작위 알고리즘'이 있습니다.

 

확률론적 소수판별법에서, 어떤 수가 

소수로 판별되면 그 수는 아마도 소수이고, 합성수로 판별되면 그 수는 무조건 합성수입니다.

이를 엄밀히 다음처럼 표현합니다. "합성수가 아니라면, 아마도 소수다"

 

4. 밀러-라빈 소수판별법

참고 : https://ko.wikipedia.org/wiki/%EB%B0%80%EB%9F%AC-%EB%9D%BC%EB%B9%88_%EC%86%8C%EC%88%98%ED%8C%90%EB%B3%84%EB%B2%95

밀러-라빈 소수판별법 - 위키백과, 우리 모두의 백과사전

밀러라빈의 시간복잡도와 관련한 부분을 발췌해보면 다음과 같습니다.

FFT는 Fast Fourier Transform, 고속 푸리에 변환입니다. 이에 대해서는 아래의 간단한 설명으로 대체합니다.

※ N개의 데이터 2개를 곱할때, O(N^2)의 시간이 소요되지만, FFT로 O(NlogN)만에 곱할 수 있습니다.

 

밀러-라빈 소수판별법을 사용하여 해결해야하는 문제가 BOJ에 있습니다.

 https://www.acmicpc.net/problem/5615 

5615번: 아파트 임대

아래는 밀러라빈 소수판별법을 구현하여 해결한 소스코드입니다.

#include<stdio.h>
typedef unsigned long long ull;
int n;
ull pow(ull x, ull y, ull p) {
    ull res = 1;
    x %= p;
    while (y > 0) {
        if (y & 1) {
            res *= x;
            res %= p;
        }
        y = y >> 1;
        x = (x * x) % p;
    }
    return res;
}
bool miller_rabin(ull n, ull a) {
    int i;
    ull r = 0;
    ull d = n - 1;
    while (d % 2 == 0) {
        r++;
        d = d >> 1;
    }
    ull x = pow(a, d, n);
    if (x == 1 || x == n - 1) return true;
    for (i = 0; i < r - 1; i++) {
        x = pow(x, 2, n);
        if (x == n - 1)
            return true;
    }
    return false;
}
bool isPrime(ull n) {
    int i;
    ull prime[5] = { 2,3,5,7,11 };
    if (n <= 1)return false;
    if (n == 2 || n == 3 || n == 5 || n == 7 || n == 11)return true;
    if (n % 2 == 0)return false;
    for (i = 0; i < 5; i++) {
        ull a = prime[i];
        if (miller_rabin(n, a) == false)
            return false;
    }
    return true;
}
int main(void) {
    int i, cnt = 0;
    ull target;
    scanf("%d", &n);
    for (i = 0; i < n; i++) {
        scanf("%lld", &target);
        if (isPrime(2 * target + 1))cnt++;
    }
    printf("%d", cnt);
}

우리가 보던 isPrime함수의 역할은 그대로입니다. n을 전달하여 n이 소수라면 true, 합성수라면 false를 반환합니다.

pow는 x,y,p를 받아 res를 반환합니다. res = (x^y)%p입니다.

miller_rabin은 밀러라빈 알고리즘의 핵심이라 부를만한 부분입니다. 이는 페르마의 소정리에 근간합니다.

페르마의 소정리

p가 소수이고 a가 정수일때, a^(p-1)을 p로 나눈 나머지는 1이다.

 

밀러라빈은 다음을 이용합니다. 아래의 두 식이 참이면 n이 소수가 아니라고 판단합니다.

 

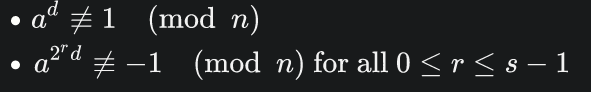
한가지 주의할점은, 합성수의 판단에 대한 부분은 결정론적이지만

소수의 판단에 대한 부분은 확률적이므로, 위 두개의 수식이 참일때에만 조기종료가 가능합니다.

 

또한 일반적으로 확률론적 알고리즘은 반례가 존재할 수 있지만, 일반적으로 작은 수에 대해서는

반례를 만들지 않도록 하는 방법이 알려진 경우가 많습니다. 역시 위키피디아에서 발췌해보면

a는 소수의 목록입니다.

isPrime()의 prime[]은 {2, 3, 5, 7 ,11}을 담고있으니 n<2,152,302,898,747 일때에는 반례가 없음을 알 수 있습니다.

 

---

<그 외 참고할만한 사실들>

 

- 일반화 리만가설이 참이면, 밀러라빈 소수판별법은 아래의 특징을 가집니다.

-> 2(logn)^2개의 a에 대해서 검사하면 반례가 없으며, 곧 O((logN)^4))의 시간복잡도를 갖는 '결정론적 알고리즘'이다

 

- 합성수를 소수로 판단할 확률은 4^(-k) 입니다. (k는 a의 개수) 이는 솔로바이-스트라센 소수판별법보다 낮습니다.

- 위에서도 설명했듯, 밀러라빈의 구현 방법에 따라 퍼포먼스차이가 존재합니다.

- a를 무작위로 생성하는 경우 밀러라빈의 정확성 및 효율성이 '무작위 생성 알고리즘'에도 큰 영향을 받습니다

- pow()는 오버플로우를 막으며 분할정복을 이용해 빠르게 계산하는 함수입니다.(분할정복을 이용한 거듭제곱)

 

---

<구간대상 소수판별>

우선, 구간대상 소수판별법이 사용되는 상황을 생각해봅시다.

입력으로 2개의 수가 들어온다면, 구간대상 소수판별법을 사용하는것은 되려 비효율적입니다.

그렇기에, 구간대상 소수판별법은 "1부터 100000까지의 모든 소수를 구하시오" 와 같은 상황에 사용합니다.

 

1. 개선된 소수판별법 + 브루트포스

앞서 O(sqrt(N))의 시간복잡도를 갖는 소수판별법에 대하여 다뤘습니다.

이를 사용해, 구간 (s, e)에 대하여 O((e-s+1)*sqrt(N))의 시간복잡도를 갖는 구간대상 소수판별법을 구현할 수 있습니다.

#include<stdio.h>
bool isPrime(int n) {
    if (n == 2)return true;
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0)return false;
    }
    return true;
}
int main(void) {
    int s = 2, e = 100;
    for (int i = s; i <= e; i++)
        if (isPrime(i))
            printf("%d : 소수\n", i);
    return 0;
}

 

 

2. 에라토스테네스의 체

 

에라토스테네스의 체는 아래처럼 구현합니다.

#include<stdio.h>
#include<algorithm>
using namespace std;
const int MAX = 1000;
bool prime[MAX + 1];
int main(void) {
    int i,j;
    fill(prime, prime + MAX + 1, true);
    prime[0] = prime[1] = false;
    for (i = 2; i * i <= MAX; i++) {
        if (prime[i] == false)continue;
        for (j = i * 2; j <= MAX; j += i)
            prime[j] = false;
    }
    return 0;
}

 

10라인의 for의 범위를 sqrt(MAX)까지로 설정하는것이 가능한 이유는

<단일대상 소수판별>의 2번 항목과 같은 이유입니다. 

물론 <단일대상 소수판별>에서 보았듯 wheel factorization을 적용하는것도 가능합니다.

에라토스테네스의 체의 시간복잡도는 O(Nlog(logN))입니다.

 

---

<소인수분해>

작은 수에대한 소인수분해는 간단히 해결할 수 있습니다.나눌수 있다면 나누고, 나눌수 없다면 다른 인수를 탐색합니다.

참고할문제는 다음과 같습니다.

https://www.acmicpc.net/problem/11653

11653번: 소인수분해

N의 범위가 천만이므로, 별도의 알고리즘 없이도 해결이 가능합니다.

#include<stdio.h>
#include<vector>
using namespace std;
vector<int>v;
void factorization(int n) {
    for (int i = 2; i * i <= n; i++) {
        while (n % i == 0) {
            n /= i;
            v.push_back(i);
        }
    }
    if (n > 1)v.push_back(n);
}
int main(void) {
    int n = 0;
    scanf("%d", &n);
    factorization(n);
    for (auto& x : v) {
        printf("%d\n", x);
    }
    return 0;
}

6라인의 for문의 조건은 역시나 sqrt(N)까지입니다.

7라인에서 나눌수 있을때까지(while) 나누어보고, 더이상 나누어지지 않으면 다음 인수를 찾아갑니다.

<단일대상 소수판별>을 이해하셨다면 위 코드도 쉽게 이해하실 수 있겠습니다.

6라인의 for문이 sqrt(N)번 반복되므로 시간복잡도는 O(N^(1/2))입니다.

 

소수의 의미에 기반한 소인수 분해를, 별도의 어려운 알고리즘을 사용하지 않고 개선해봅시다.

구간 [2, e]의 수 k에 대하여, k의 가장 작은 인수를 모두 구해놓는 방법입니다.

다만 k가 소수인 경우에는 1이 아닌 k를 저장합니다. 이는 아래처럼 구현합니다.

void init(void) {
    int i, j;
    for (i = 0; i <= MAX; i++)
        initPrime[i] = i;
    for (i = 2; i <= MAX; i++) {
        if (initPrime[i] != i)continue;
        for (j = 2;; j++) {
            if (i * j > MAX)break;
            initPrime[i * j] = i;
        }
    }
}

참고 : https://rebro.kr/96

PS를 위한 정수론 - (1) 에라토스테네스의 체 활용

이 방법을 사용하여, 구간대상 소인수분해의 시간복잡도를

O(N*sqrt(N))에서 O(NlogN)으로 최적화가 가능합니다.

#include<bits/stdc++.h>
using namespace std;
 
const int MAX = 500000;
int initPrime[MAX + 1];
 
void init(void) {
    int i, j;
    for (i = 0; i <= MAX; i++)
        initPrime[i] = i;
    for (i = 2; i <= MAX; i++) {
        if (initPrime[i] != i)continue;
        for (j = 2;; j++) {
            if (i * j > MAX)break;
            initPrime[i * j] = i;
        }
    }
}
vector<int> initFactorization(int n) {
    int i;
    vector<int>v;
    //v.clear();
    int cur = n;
    while (cur > 1) {
        v.push_back(initPrime[cur]);
        cur /= initPrime[cur];
    }
    return v;
}
vector<int> factorzation(int n) {
    vector<int>v;
    int i;
    int cur = n;
    for (i = 2; i * i <= n; i++) {
        while (cur % i == 0) {
            cur /= i;
            v.push_back(i);
        }
    }
    if (cur > 1)v.push_back(cur);
    return v;
}
bool isPrime(int n) {
    if (n <= 1)return false;
    if (n == 2)return true;
    for (int i = 2; i * i <= n; i++)
        if (n % i == 0)return false;
    return true;
}
vector<int> init_primeExecpetion_Factorization(int n) {
    int i;
    vector<int>v;
    if (isPrime(n) == true) {
        v.push_back(n);
        return v;
    }
    int cur = n;
    while (cur > 1) {
        v.push_back(initPrime[cur]);
        cur /= initPrime[cur];
    }
    return v;
}
vector<int> primeException_Factorzation(int n) {
    vector<int>v;
    if (isPrime(n) == true) {
        v.push_back(n);
        return v;
    }
    int i;
    int cur = n;
    for (i = 2; i * i <= n; i++) {
        while (cur % i == 0) {
            cur /= i;
            v.push_back(i);
        }
    }
    if (cur > 1)v.push_back(cur);
    return v;
}
int main(void) {
    int i, j;
    clock_t start, end;
 
    start = clock();
    init();
    for (i = 2; i <= MAX; i++) {
        vector<int>result = initFactorization(i);
    }
    end = clock();
    printf("init factorization : %f\n", (double)end - start);
 
    start = clock();
    for (i = 2; i <= MAX; i++) {
        vector<int>result_2 = factorzation(i);
    }
    end = clock();
    printf("plain factorization : %f\n", (double)end - start);
    
    start = clock();
    for (i = 2; i <= MAX; i++) {
        vector<int>result_3 = primeException_Factorzation(i);
    }
    end = clock();
    printf("prime exception : %f\n", (double)end - start);
 
    start = clock();
    init();
    for (i = 2; i <= MAX; i++) {
        vector<int>result_4 = init_primeExecpetion_Factorization(i);
    }
    end = clock();    
    printf("init prime exception : %f\n", (double)end - start);
    return 0;
}

소수를 소인수분해하지 않도록 예외처리하는 부분과, 구간의 최소 인수를 미리 구해놓는(전처리) 부분으로

최적화가 가능합니다. 

이 밖에도 

1. isPrime()을 밀러-라빈기반의 알고리즘으로 변경

2. push_back같은 무거운 연산 대신 가벼운 연산으로 변경하여 상수최적화

...와 같은 방법을 사용하여, 어느정도 개선해볼 여지가 있겠습니다.

 

이제 위 문제를 확장해보겠습니다. 

https://www.acmicpc.net/problem/4149

4149번: 큰 수 소인수분해

이글에서 다룬 모든 알고리즘을 확장시켜 해결할 수 있습니다. 알고리즘의 이름은 폴라드로 알고리즘입니다.

https://ko.wikipedia.org/wiki/%ED%8F%B4%EB%9D%BC%EB%93%9C_%EB%A1%9C_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

폴라드 로 알고리즘 - 위키백과, 우리 모두의 백과사전

 

폴라드로 알고리즘을 구현하면 문제의 대부분을 해결한 셈이지만

long long과 long long을 곱하는 과정중 오버플로우가 발생하기에 __int128을 사용해야 합니다.

다만 이는 컴파일러에 의존적이므로, 오버플로우가 발생하지만 작은 입력에 대해서는 정상적인 코드를 대신 첨부합니다.

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<vector>
#include<algorithm>
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
vector<ll>v;
ll _gcd(ll a, ll b) {
    if (a < b)swap(a, b);
    ll c = 0;
    while (b != 0) {
        c = a % b;
        a = b;
        b = c;
    }
    return a;
}
ull pow(ull x, ull y, ull p) {
    ull res = 1;
    x %= p;
    while (y > 0) {
        if (y & 1) {
            res *= x;
            res %= p;
        }
        y = y >> 1;
        x = (x * x) % p;
    }
    return res;
}
bool millerRabin(ull n, ull a) {
    int i;
    ull r = 0;
    ull d = n - 1;
    while (d % 2 == 0) {
        r++;
        d = d >> 1;
    }
    ull x = pow(a, d, n);
    if (x == 1 || x == n - 1) return true;
    for (i = 0; i < r - 1; i++) {
        x = pow(x, 2, n);
        if (x == n - 1)
            return true;
    }
    return false;
}
bool isPrime(ull n) {
    int i;
    ull prime[30] = { 2,3,5,7,11,13,17,19,23,29,31,37,41 };//13개
    if (n <= 1)return false;
    if (n == 2 || n == 3)return true;
    if (n % 2 == 0)return false;
    for (i = 0; i < 13; i++) {
        ull a = prime[i];
        if (n == a)return true;
        if (millerRabin(n, a) == false)
            return false;
    }
    return true;
}
ll pollardRho(ll n) {
    if (isPrime((ull)n))return n;
    srand(time(NULL));
    if (n == 1)return n;
    if (n % 2 == 0)return 2;
    ll x = (rand() % (n - 2)) + 1;
    ll y = x;
    ll c = (rand() % (n - 1)) + 1;
    ll d = 1;
    while (d == 1) {
        x = (pow((ull)x, (ull)2, (ull)n) + c + n) % n;
        y = (pow((ull)y, (ull)2, (ull)n) + c + n) % n;
        y = (pow((ull)y, (ull)x, (ull)n) + c + n) % n;
        d = _gcd(abs(x - y), n);
        if (d == n) {
            return pollardRho(n);
        }
    }
    if (isPrime(d))return d;
    else return pollardRho(d);
}
int main(void) {
    ll num;
    scanf("%lld", &num);
    while (num > 1) {
        ll d = pollardRho(num);
        v.push_back(d);
        num /= d;
    }
    sort(v.begin(), v.end());
    int S = v.size();
    for (int i = 0; i < S; i++)
        printf("%lld\n", v[i]);
    return 0;
}

※ 위 코드는 아직 오버플로우 문제가 해결되지 않았습니다.

※ gcd는 stl도 있습니다. 위 코드는 유클리드 알고리즘으로 구현하였습니다.

 

pollardRho()함수를 제외하고는 밀러라빈 소수판별법에서 이미 다루었습니다.

소인수분해를 하는데에 소수판별이 들어가는 이유는,

매우 큰 소수가 폴라드로함수의 인수로 들어가는걸 막기 위함입니다.

폴라드로 알고리즘의 인수로 전달되는, 즉 소인수분해를 할 숫자를 N이라고 할때

폴라드로 알고리즘의 시간복잡도는 N의 가장 작은 소인수의 제곱근에 비례하고

이는 최악의 경우에도 O(N^(1/4))입니다. 다만 이는 N이 합성수일때의 시간복잡도이고,

N이 소수인 경우에는 O(N)의 시간이 소요되거나 무한루프에 빠질수도 있습니다.

꼭 소수판별법과 함께 사용하여 인수로 소수가 전달되지 않아야합니다.

 

---

<같이보면 좋은것>

- 생일 문제(생일 역설)

- 플로이드 사이클 탐지(토끼와 거북이 알고리즘, Floyd's cycle dectection)